A brief mathematical biography
I graduated from UC Berkeley in May 2008, where my advisor was Nicolai Reshetikhin. I then
spent a year working with
Arun Ram in Melbourne
Australia and three years as an NSF postdoctoral fellow and CLE Moore Instructor at MIT. As of August 2012, I am an assistant professor at Loyola
University in Chicago.
My research is mostly about quantum groups and related combinatorics, particularly
quantum affine algebras. Recently I have also been working with quiver varieties and with Khovanov-Lauda-Rouquier algebras.
Below you can find brief descriptions of some of my main projects.
This is not an exhaustive list of my work; some of my papers do not fit nicely into these holes, and so are not mentioned here.
You can also find more information in my
CV and related documents.
I am most interested in crystals, which in this context are combinatorial objects associated to (usually highest weight) representations of a complex simple Lie algebra,
or more generally a symmetrizable Kac-Moody algebra.
They record certain leading order data of the representation theory, and can be used to give
combinatorial answers to various representation theoretic questions, such as calculating tensor product multiplicities.
They also let you draw nice pictures:
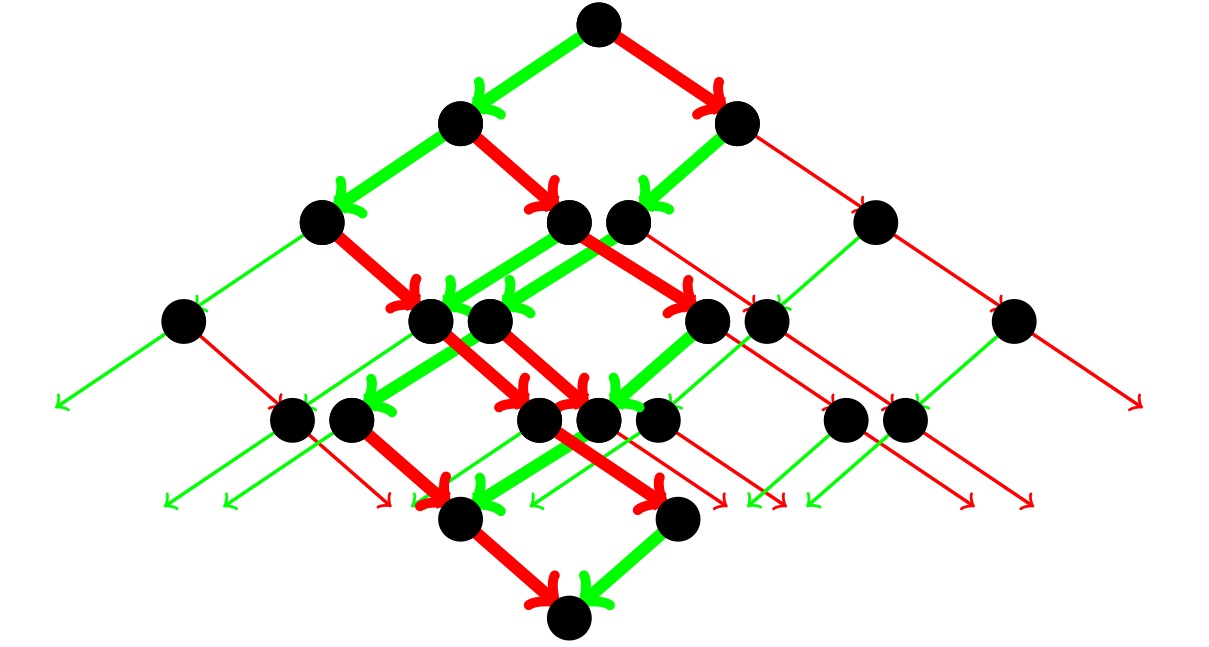
Affine MV polytopes
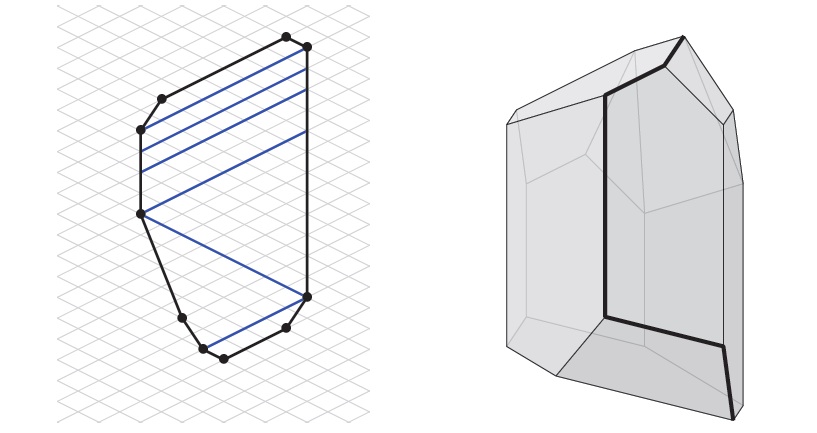
Mirkovic-Vilonen (MV) polytopes were developed by Anderson and by Kamnitzer
as moment map images of certain cycles in an affine grassmannian. They can be
used to realize the crystal of any finite dimensional representation of a
complex simple Lie algebra. The polytopes encode a great deal of information, and show up in several natural contexts.
For instance, as well as with the affine grassmannian, they have natural
relationships with Lusztig's PBW bases,
with quiver varieties, and (very recently) with
Khovanov-Lauda-Rouquier (KLR) algebras.
This project develops an analogue of this theory in affine types.
- In Affine Mirkovic-Vilonen polytopes, with Pierre Baumann and Joel Kamnitzer, we use quiver varieties to define MV polytopes in symmetric affine types.
These affine MV polytopes consist of underlying polytopes in the affine root lattice, decorated with the extra data of a partition associated to certain co-dimension 1 faces.
They record the dimensions of all submodules of certain generic modules of the preprojective algebra.
We also show that, as in the finite type situation, classifying MV polytopes reduces to classifying the rank 2 cases. These polytopes can be used to realize all highest weight crystals just as in the finite type sutuation.
- In Rank 2 affine MV polytopes, with Pierre Baumann, Thomas Dunlap and Joel Kamnitzer, we give a combinatorial definition of MV polytopes for the two rank 2 affine algebras. We show that these can be used to realize highest weight crystals as expected. We conjecture that, in the affine sl(2) case, these essentially agree with the polytopes defined in the previous paper.
- In ongoing work with Dinakar Muthiah, we show that rank 2 affine MV polytopes are related to affine PBW bases (as defined by Beck-Chari-Pressley and Beck-Nakajima) in the same way that finite type MV polytopes are related to ordinary PBW bases. We also show that the two realizations of affine sl(2) MV polytopes mentioned above agree (after a small change of conventions). This completes the combinatorial characterization of symmetric affine MV polytopes.
- In ongoing work with Ben Webster we develop a relationship between MV polytopes and irreducible representations of Khovanov-Lauda-Rouquier algebras. In finite type this is a slight strengthening and rewording of a result of Kleshchev-Ram: the MV polytope corresponding to an irreducible representation is the convex hull of the words which appear with non-zero coefficient in its character. In affine type the underlying polytope is defined in the same manner, but we need to do some more work to describe the partitions decorating the faces. Using this relationship we are able to understand MV polytopes in all (not necessarily symmetric) affine cases.
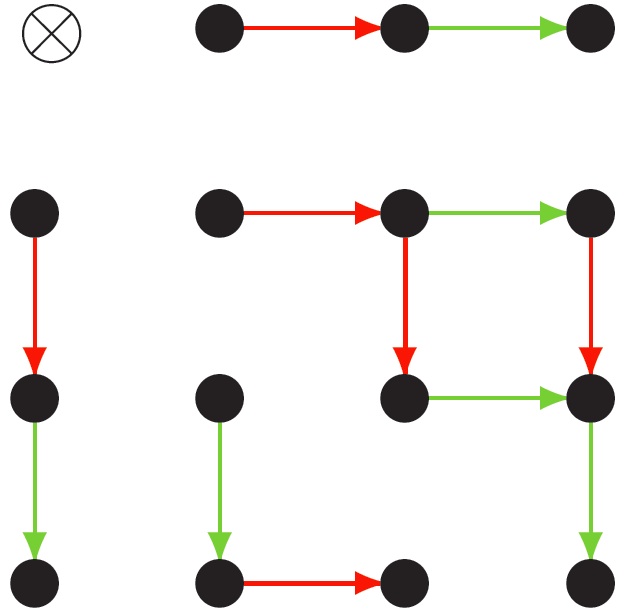
The crystal commutor and the half twist
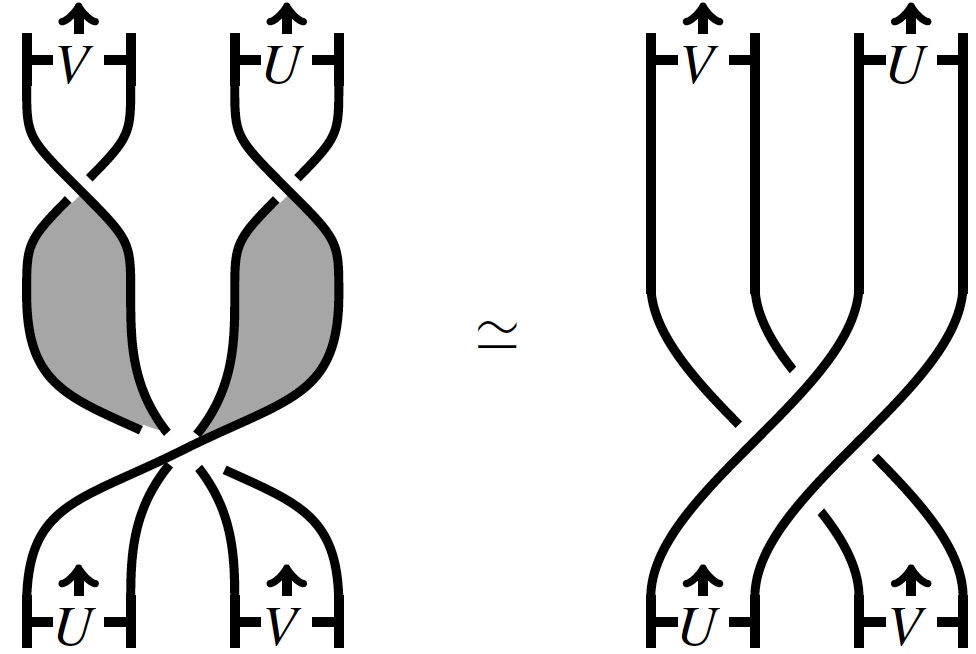
One important property of the category of representations of a quantized universal enveloping algebra is that it is braided: there is a family of isomorphisms \( V \otimes W \rightarrow W \otimes V \) such that the action on any n-fold tensor product factors through the n-strand braid group. One might hope this descends to a braiding on the category of crystals, but it cannot. In fact it is easy to see that there is no braiding on the category of crystals.
However, there is a related structure: the crystal commutor of Henriques-Kamnitzer. There the braid group is replaced by the fundamental group of the moduli space of marked real genus zero stable curves (sometimes called the cactus group).
-
In A definition of the crystal commutor using Kashiwara's involution, with Joel Kamnitzer, we extend the definition of the crystal commutor from finite type to all symmetrizable Kac-Moody algebras. We do not show that this has the properties discussed above, but this was later established by Alistair Savage (using quiver varieties).
-
In The crystal commutor and Drinfeld's unitarized R-matrix, with Joel Kamnitzer, we show how the crystal commutor is in fact a limit of a structure on the category of representations; Drinfeld's unitarized R-matrix. This makes precise the notion that the crystal commutor is the combinatorial shadow of the braiding.
-
In The half-twist for \(U_q(g)\) representations, with Noah Snyder, we study some topological implications of
these ideas.
The previous paper uses a formula for the R-matrix of the form \( R= (X \circ X) \Delta(X
)^{-1} \).
We introduce the notion of a "half-twist" hopf algebra which is essentially a quasi-triangular Hopf algebra with an element X related to the \(R\) matrix as above.
We discuss how this formula is an algebraic version of the picture at the start of this section, where
where X corresponds to the 180 degree twist (i.e. the half twist). This also sheds light on some sign issues in relating different constructions of the Jones polynomial, which I discuss in the expository notes A minus sign that used to annoy me but now I know why it is there
- In A formula for the R-matrix using a system of weight preserving endomorphisms I realize the R-matrix using a modification of the half-twist.
This has the advantage that the formula makes sense in all types, although I only show it actually gives the R-matrix in finite type.
- In the unpublished work A half-twist type formula for the R-matrix of a symmetrizable Kac-Moody algebra I modify the definitions in the previous paper to get a version of the half twist that does give rise to the R-matrix is all types.
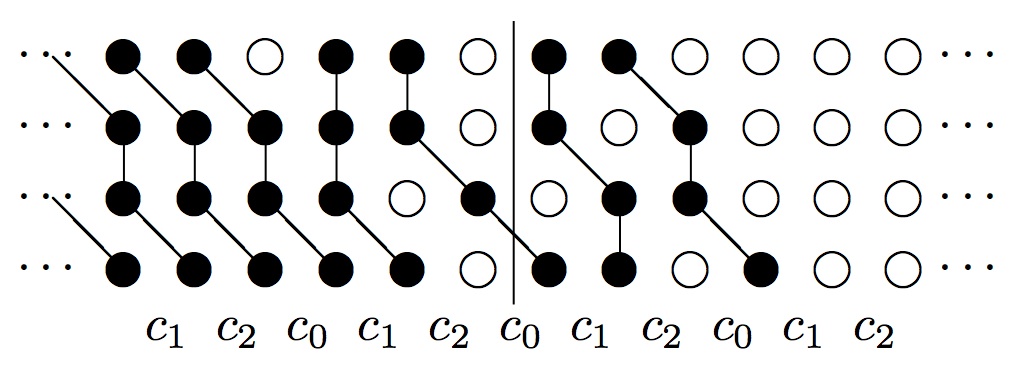
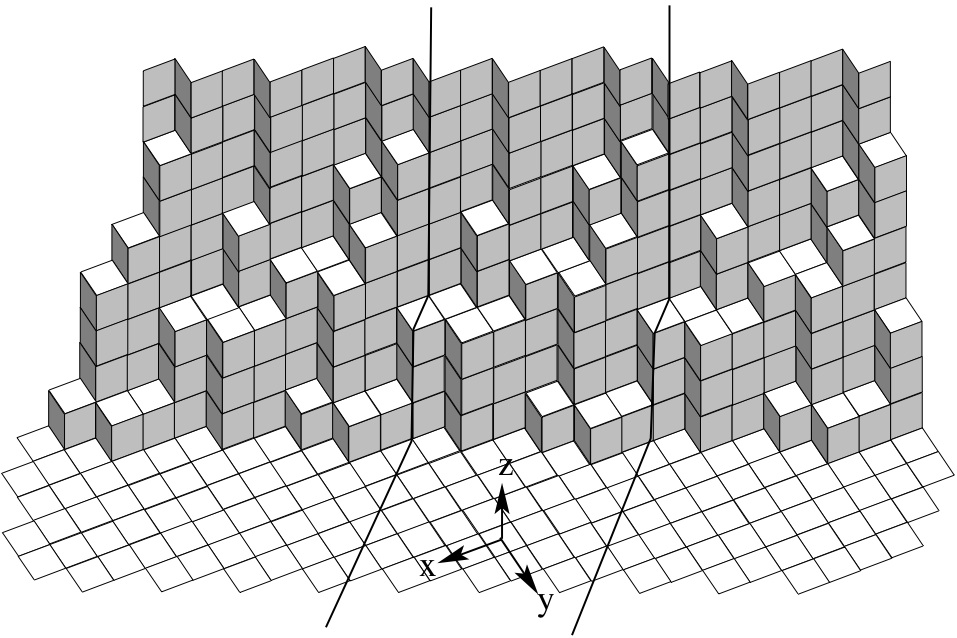
Constructing and relating various realization of affine sl(n) crystals
The goal of this project (which formed the bulk of my thesis) was to have a
concrete understanding of affine
sl(n) crystals, and to understand how seemingly different realizations of those crystals were related.
The early work was combinatorial, but the project has more recently
used quite a bit of geometry, in particular the quiver varieties of Lusztig and Nakajima.