Advanced Biostatistics Chapter 7: Nonlinear Regression with AR1 Errors 17 April 2006

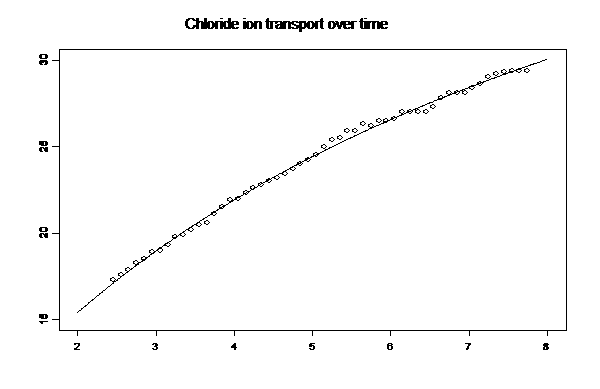
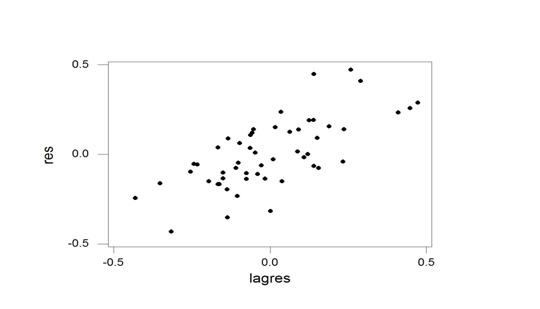
The above mean curve suggests LL3 model function, , and plot of Residuals versus Lagged-Residuals suggests AR(1) time series error structure, e_t = fe_t-1 + a_t, -1 < f < 1, where the a_t are assumed to be independent N(0,s²).

Independent LL3 Model

start neg2lla(th) global(xx,yy,nn);

th1=th[1]; th2=th[2]; th3=th[3]; sig=th[4]; sig2=sig*sig;

tt=xx/th3; den=1+tt; eta=th1+(th2-th1)/den; res=yy-eta;

thingy=nn*log(sig2)+(1/sig2)*t(res)*res;

return(thingy);

finish neg2lla;

MINN2LLA = -124.5789

THA SESA

54.299768 1.384656

5.6606322 0.4736729

7.9605237 0.5770078

0.1913774 0.0130267

AR(1) LL3 Model

start neg2llb(th) global(xx,yy,nn);

th1=th[1]; th2=th[2]; th3=th[3]; sig=th[4]; rho=th[5]; sig2=sig*sig;

omr2=1-rho**(0.20); sig2a=sig2*omr2; tt=xx/th3; den=1+tt;

eta=th1+(th2-th1)/den; res=yy-eta; rest=res[2:nn,]; ress=res[1:(nn-1),];

resp=rest-(rho**(0.10))*ress;

thingy=nn*log(sig2a)-log(omr2)+(1/sig2a)*( omr2*res[1]*res[1]+t(resp)*resp );

return(thingy);

finish neg2llb;

MINN2LLB = -159.3582

THB SESB

54.214864 2.72031

5.8524633 0.8959594

8.0248275 1.13469

0.1930062 0.0222893

0.0282681 0.0279577

For these data, f is estimated to be 0.0283, and the LR test of f = 0 is soundly rejected (c₁² = –2DLL = 34.78, p < 0.0001).

Note too that the SE’s associated with the LD₅₀ approximately doubles as we move from the independent LL3 model to the AR(1) LL3 model.

Independent LL3 Model

AR(1) LL3 Model

For these data, f is estimated to be 0.0283, and the LR test of f = 0 is soundly rejected (c12 = –2DLL = 34.78, p < 0.0001).

Note too that the SE’s associated with the LD50 approximately doubles as we move from the independent LL3 model to the AR(1) LL3 model.

For these data, f is estimated to be 0.0283, and the LR test of f = 0 is soundly rejected (c₁² = –2DLL = 34.78, p < 0.0001).

Note too that the SE’s associated with the LD₅₀ approximately doubles as we move from the independent LL3 model to the AR(1) LL3 model.