Advanced Biostatistics Quiz 5 Name
________________________________________
Directions:
Thoroughly, clearly and neatly answer the following two problems in the
space given, showing all relevant calculations.
Unless otherwise noted, use a = 5% throughout.
1. (1 + 1 + 3 + 1 = 5 or 6
points) The Finney4 model is
fit in the “First NLMixed” on p.3 in the Appendix to the ethanol
(denoted “eth”) and chloral hydrate (denoted “chy”) data given in Carter et
al (1988) and for which the binary response is related to the loss of
righting reflex in mice. A reduced model
is fit in the “Second NLMixed” and an extended model is fit in the “Third
NLMixed”, the latter model being useful just for part (d) below.
(a) The q2 parameter (denoted “th2”) is estimated to be
4130.47 for these data. Briefly and
clearly interpret this parameter estimate.
(b) The q4 parameter (denoted “th4”) is estimated to be
12.2530 for these data. Briefly and
clearly interpret this parameter estimate.
(c) Using the best test procedure,
characterize the interaction (if any) of ethanol and chloral hydrate, listing
hypotheses, the test statistic, degrees of freedom (dfs), p-value, and your
clear interpretation and justification.
Null hypothesis ________________________________________________
Alternative hypothesis ________________________________________________
Calculated test statistic,
distribution and dfs _________________________________________________
p-value
________________________________
detailed conclusion
(d) [Graduate
students only] The “Third NLMixed” is useful to help
determine the indicated scale for these data.
Clearly interpret the results and comment on whether the scale used in
the “First NLMixed” was well-chosen.
2. (1 + 2 + 1 + 1 = 4 or 5
points) The data analyzed on pp.4-5 of
the Appendix, reported in Millard & Krause (2001:19), correspond to canine
prostate size for 5 dogs randomized to the control group (denoted “contg”) and
5 dogs randomized to the estradiol group (denoted “estrg”), and for which
relative potency of these drugs is to be assessed using a direct assay. These data are analyzed using NLIN (p.4) and
using two runs of NLMixed (p.5)
(a) The best analysis for these data is (circle one): the NLIN the first NLMixed the second NLMixed
(b) Using the best analysis for these data, test whether the two drugs are equally potent.
Null hypothesis ________________________________________________
Alternative hypothesis ________________________________________________
detailed conclusion (including your justification)
(c) Why are the analyses not chosen in part (a) above incorrect for these data?
(d) [Graduate students only] Explain why the variance in the Second NLMixed (p.5) is written in the given form; give the justification. What are the variances for the two groups?
Advanced Biostatistics Quiz
5 Addendum
First Exercise – Programs and Output
First NLMixed
|
proc nlmixed data=one; parms th2=4150 th3=25 th4=10 th5=0;
z=eth+th4*chy+th5*sqrt(th4*eth*chy);
t=(z/th2)**th3; den=1+t; p=t/den; model y~binomial(n,p); run; |
|
The
NLMIXED Procedure Fit
Statistics -2 Log
Likelihood 57.7
Parameter Estimates Parameter
Estimate Std Error DF
t Value Pr > |t| Alpha
Lower Upper Gradient th2
4130.47 64.8087 39
63.73 <.0001 0.05
3999.38 4261.56 -2.21E-9 th3
20.1149 3.3433 39
6.02 <.0001 0.05
13.3524 26.8775 1.728E-8 th4
12.2530 0.3324 39
36.86 <.0001 0.05
11.5806 12.9254 8.748E-7 th5 0.1338 0.05704 39 2.35 0.0241 0.05 0.01846 0.2492 2.586E-6 |
Second NLMixed
|
proc nlmixed data=one; parms th2=4150 th3=25 th4=10;
z=eth+th4*chy;
t=(z/th2)**th3; den=1+t; p=t/den; model y~binomial(n,p); run; |
|
The
NLMIXED Procedure Fit Statistics -2 Log
Likelihood 63.6
Parameter Estimates Parameter
Estimate Std Error DF
t Value Pr > |t| Alpha
Lower Upper Gradient th2
4076.97 65.7330 39
62.02 <.0001 0.05
3944.01 4209.93 -1.09E-8 th3
18.9735 3.2256 39
5.88 <.0001 0.05
12.4492 25.4978 2.037E-7 th4 12.5168 0.3407 39 36.74 <.0001 0.05 11.8276 13.2059 -2.81E-6 |
Third NLMixed
|
proc nlmixed data=one; parms th2=4150 th3=25 th4=10 th5=0 th6=0.1;
z=eth+th4*chy+th5*sqrt(th4*eth*chy);
zt=(z**th6-1)/th6; th2t=(th2**th6-1)/th6;
ex=exp(th3*(zt-th2t)); den=1+ex; p=ex/den; model y~binomial(n,p); run; |
|
The
NLMIXED Procedure Fit
Statistics -2 Log
Likelihood 57.5 Parameter
Estimates Standard Parameter
Estimate Error DF
t Value Pr > |t| Alpha
Lower Upper Gradient th2
4123.50 64.8967 39
63.54 <.0001 0.05
3992.23 4254.76 -0.00169 th3
47.1676 152.51 39
0.31 0.7588 0.05
-261.30 355.64 -0.00199 th4
12.2378 0.3328 39
36.77 <.0001 0.05
11.5647 12.9109 0.000684 th5
0.1327 0.05713 39
2.32 0.0256 0.05
0.01709 0.2482 0.001336 th6 -0.1024 0.3872 39 -0.26 0.7928 0.05 -0.8856 0.6808 0.005869 |
Second Exercise – Programs and Output
NLIN run
|
data one; input group$ size @@;
contg=(group='cont'); estrg=(group='estr'); datalines; cont
1.975 cont 3.125 cont 4.433
cont 6.154 cont 4.175 estr 10.356 estr 6.313 estr 21.708 estr
12.651 estr 15.464 ; proc nlin data=one; parms mu1=1 rho=1;
mean=mu1*contg+mu1*rho*estrg; model size=mean; output out=two r=r p=p; run; |
|
The NLIN Procedure Dependent
Variable size Method:
Gauss-Newton
Sum of Mean Approx Source DF Squares Square F Value
Pr > F Model 1 217.4 217.4 12.16
0.0082 Error 8 143.0 17.8755 Corrected Total 9
360.4
Approx Parameter Estimate Std Error Approximate 95% Confidence Limits mu1 3.9724 1.8908 -0.3878 8.3326 rho 3.3477 1.6630 -0.4873 7.1827 Approximate
Correlation Matrix
mu1 rho mu1 1.0000000 -0.9581651 rho -0.9581651 1.0000000 |
Residual Plot
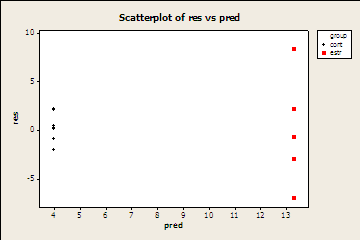
First NLMixed
|
proc nlmixed data=one; parms mu1=1 rho=1 sig=1; mean=mu1*contg+mu1*rho*estrg;
var=sig*sig; model size~normal(mean,var); run; |
|
The
NLMIXED Procedure Fit
Statistics -2 Log
Likelihood 55.0 AIC (smaller is
better) 61.0 AICC (smaller is
better) 65.0 BIC (smaller is
better) 61.9
Parameter Estimates Standard Parameter
Estimate Error DF
t Value Pr > |t| Alpha
Lower Upper Gradient mu1
3.9724 1.6912 10
2.35 0.0407 0.05
0.2042 7.7406 -2.2E-6 rho
3.3477 1.4875 10
2.25 0.0481 0.05
0.03345 6.6619 -4.96E-6 sig 3.7816 0.8456 10 4.47 0.0012 0.05 1.8975 5.6657 6.346E-7 |
Second NLMixed
|
proc nlmixed data=one; parms mu1=1 rho=1 sig=1; mean=mu1*contg+mu1*rho*estrg;
var=sig*sig*(contg+rho*rho*estrg); model size~normal(mean,var); run; |
|
The
NLMIXED Procedure Fit
Statistics -2 Log
Likelihood 48.2 AIC (smaller is
better) 54.2 AICC (smaller is
better) 58.2 BIC (smaller is
better) 55.1
Parameter Estimates Standard Parameter
Estimate Error DF
t Value Pr > |t| Alpha
Lower Upper Gradient mu1
3.9299 0.6112 10
6.43 <.0001 0.05
2.5680 5.2919 -8.08E-6 rho
3.4209 0.7091
10 4.82 0.0007
0.05 1.8409 5.0008
-8.65E-6 sig 1.4535 0.3582 10 4.06 0.0023 0.05 0.6553 2.2517 -9.74E-6 |